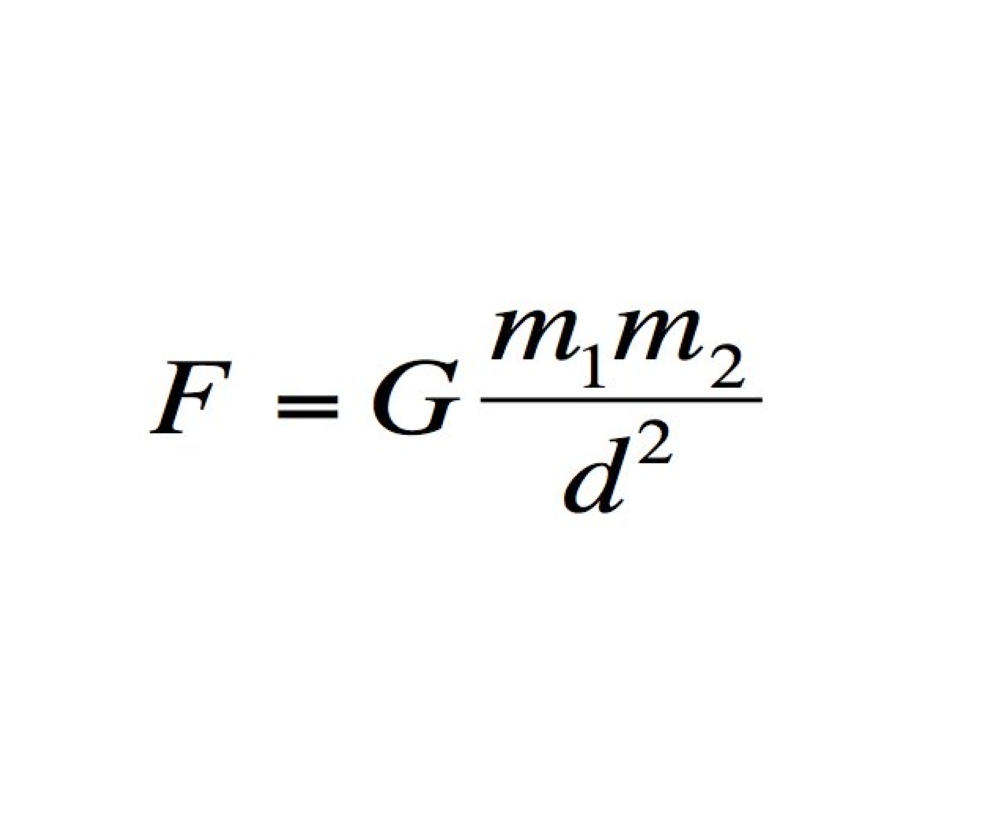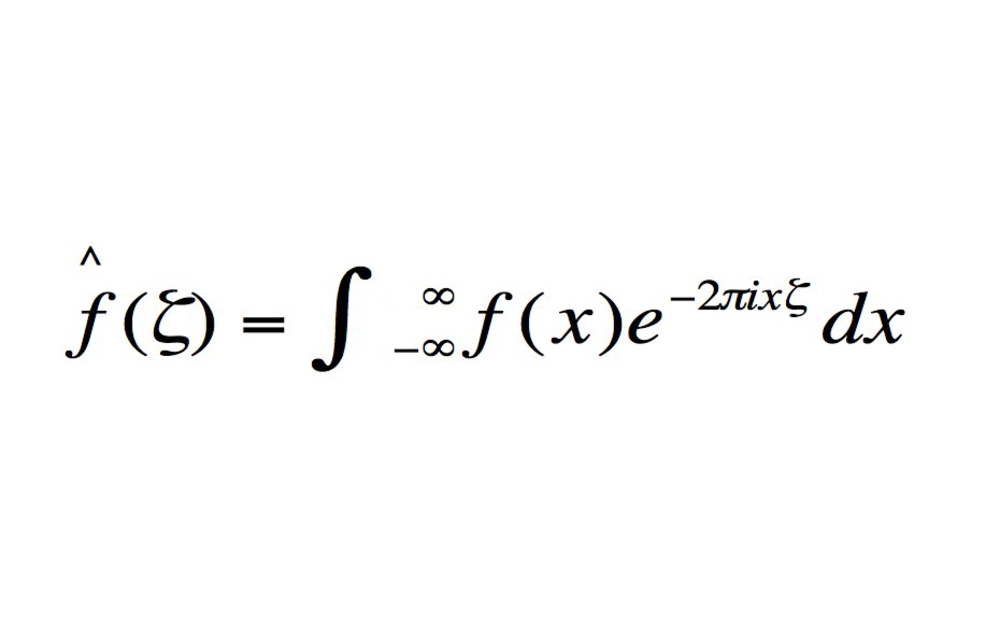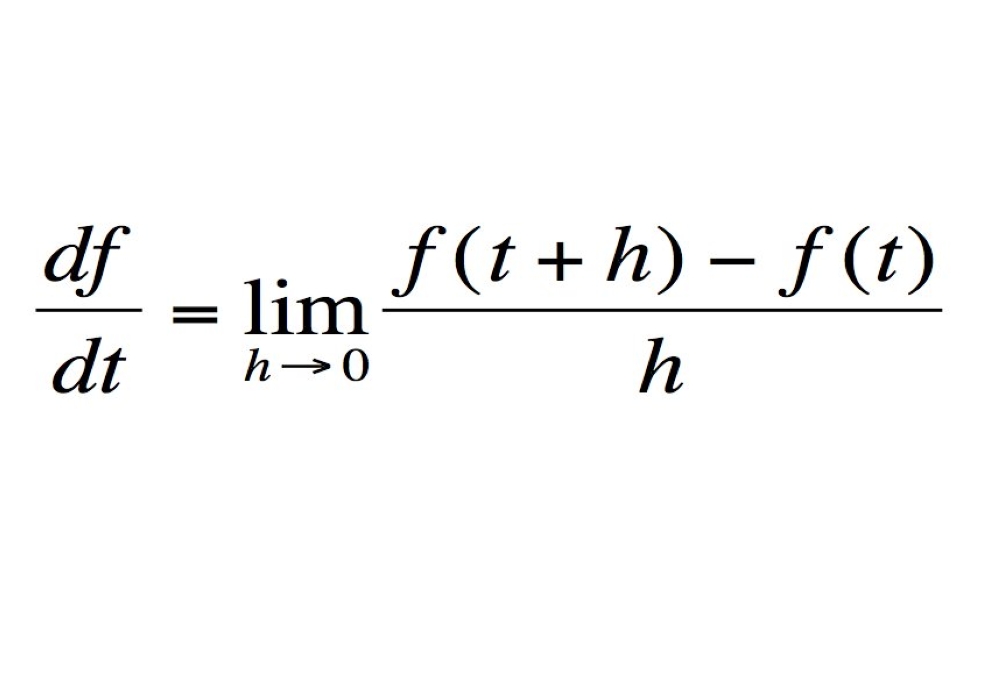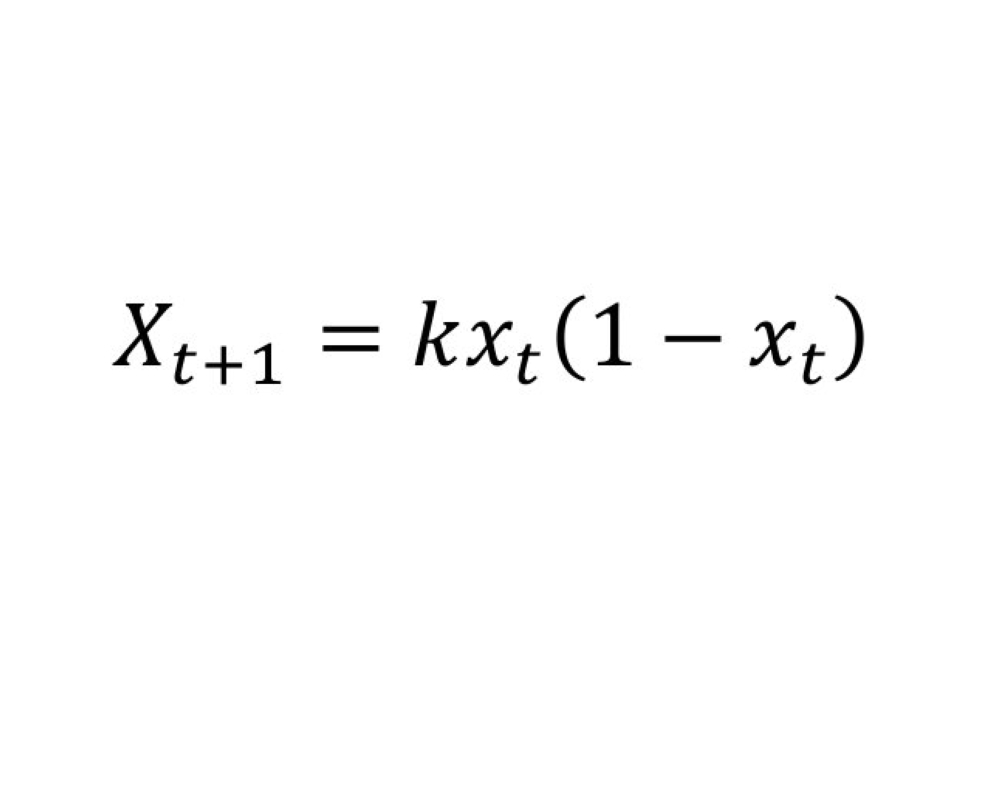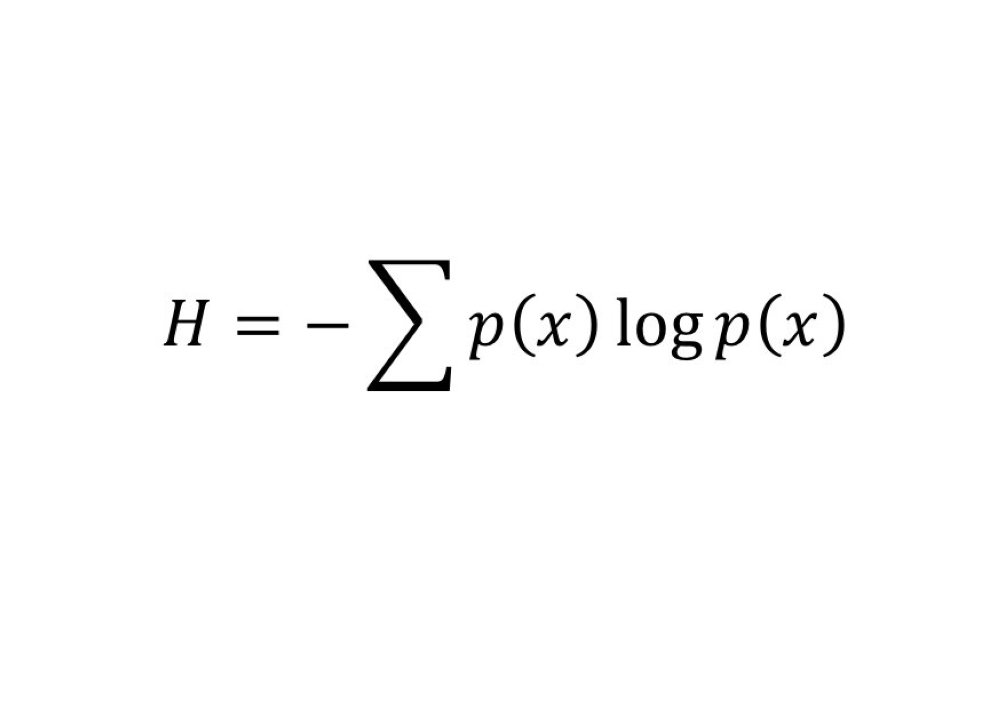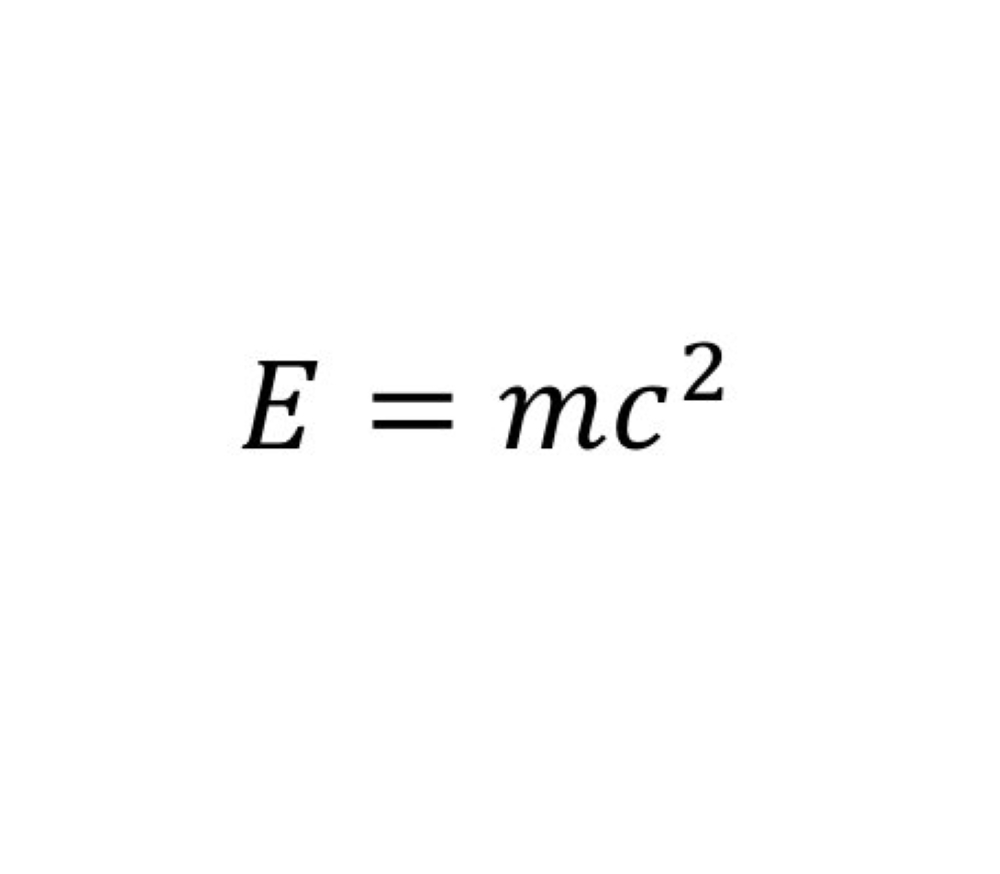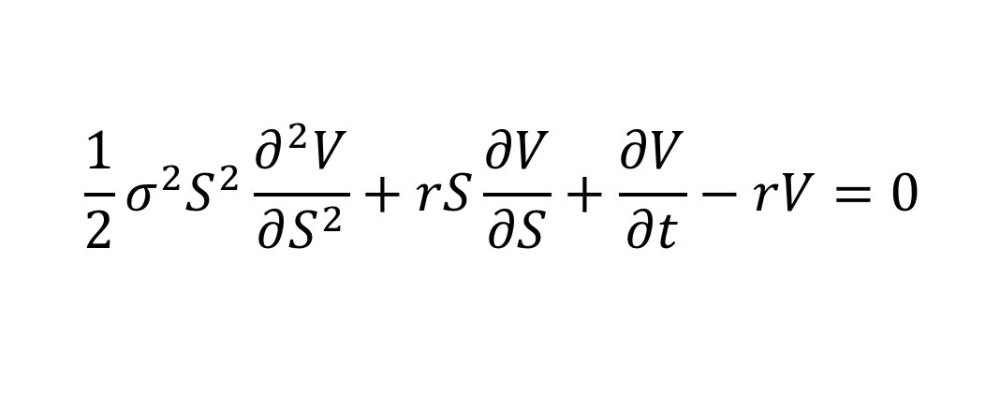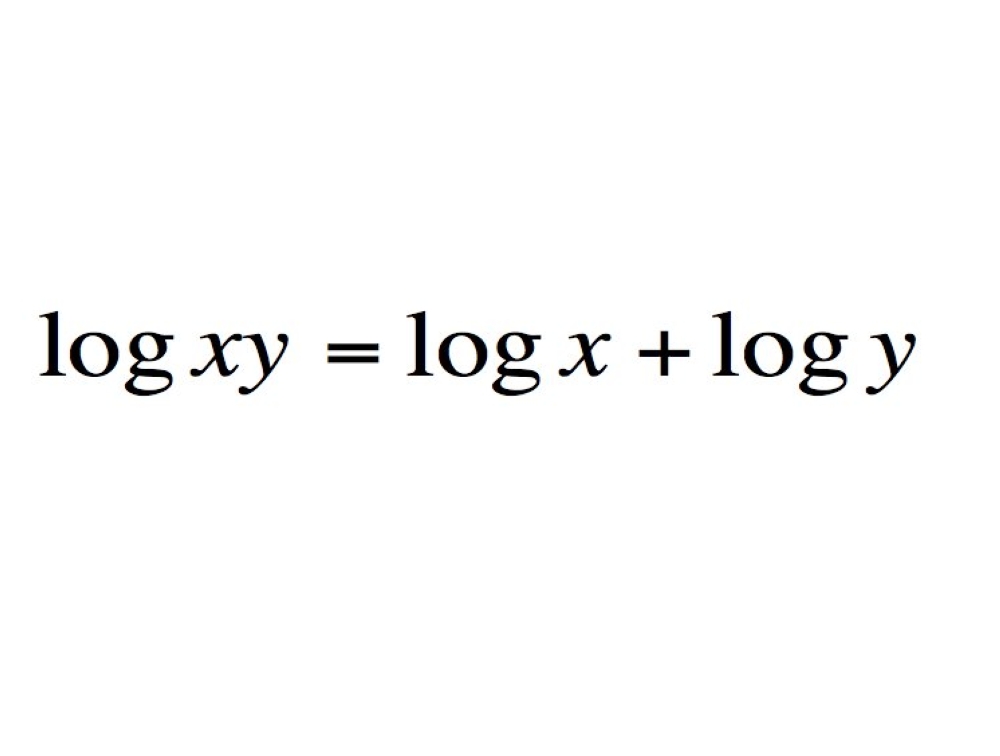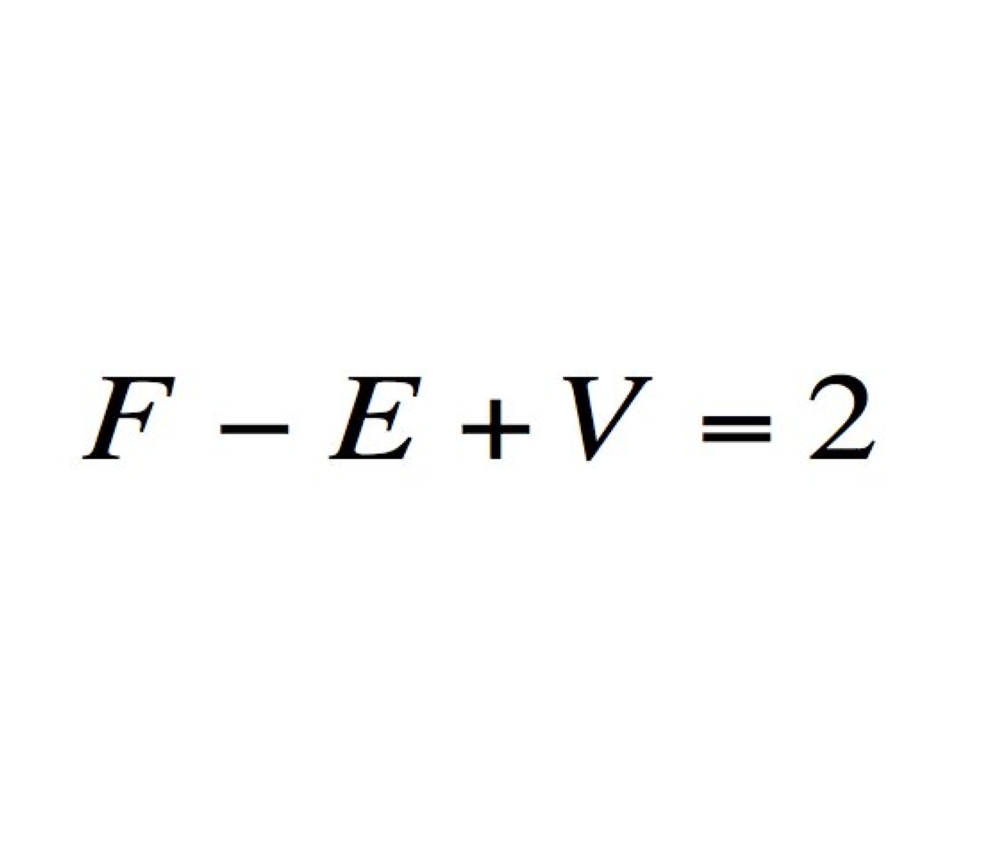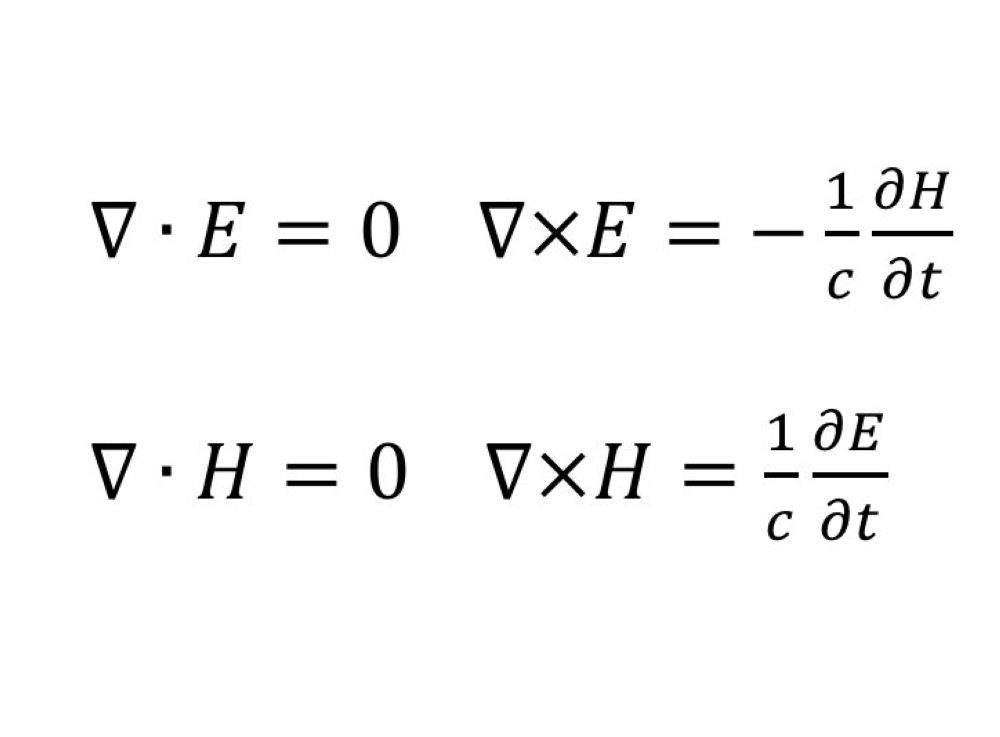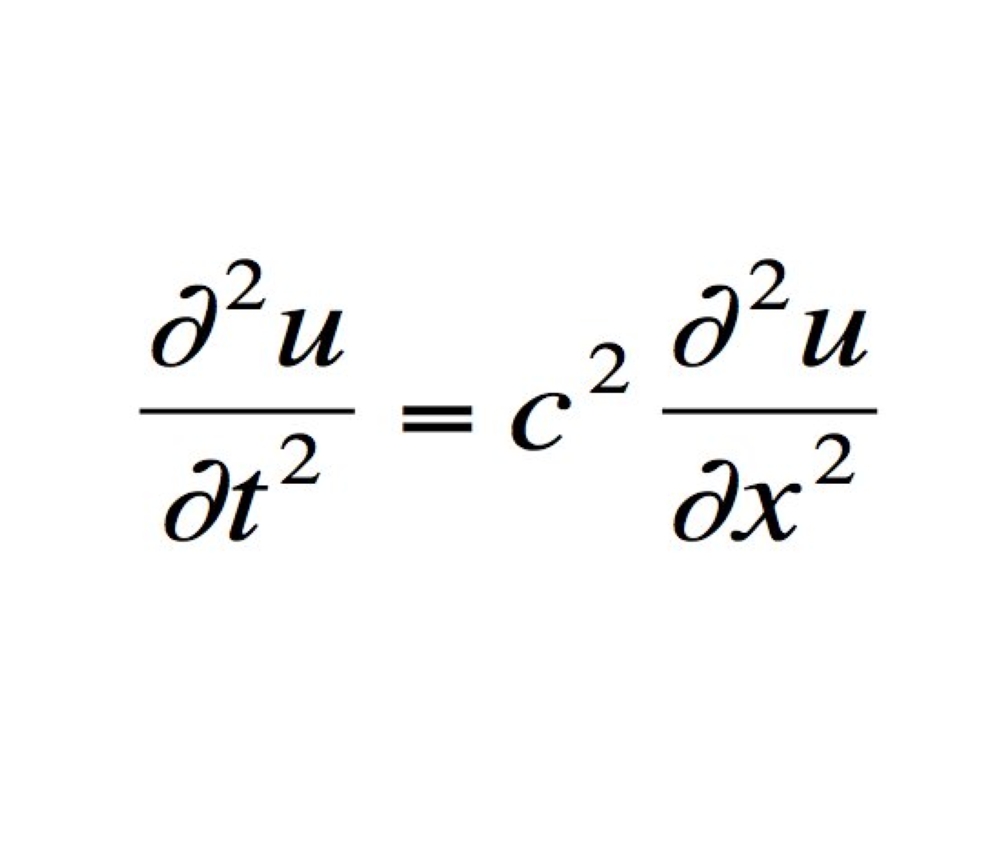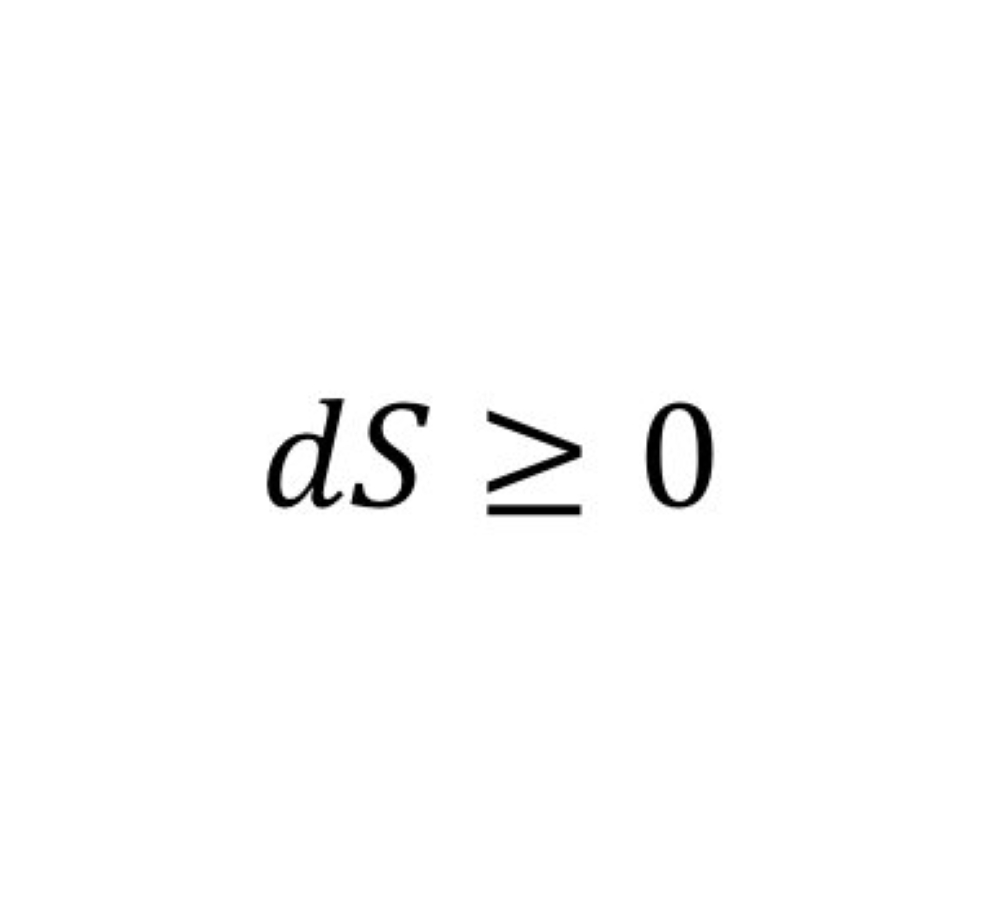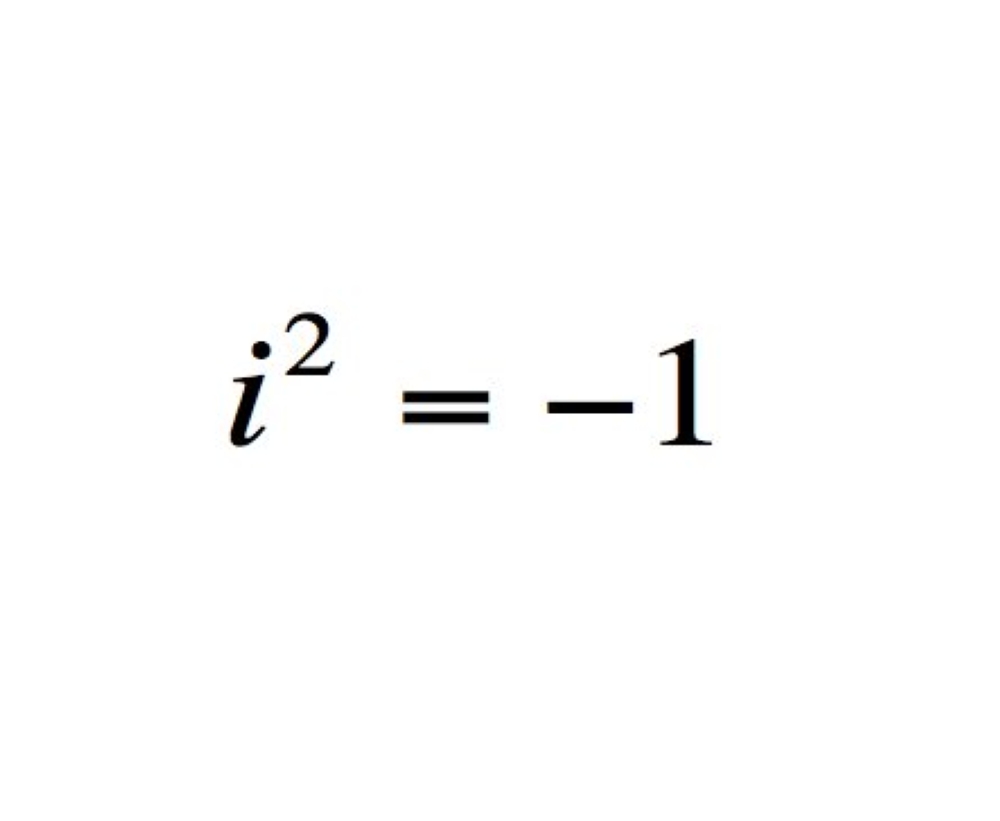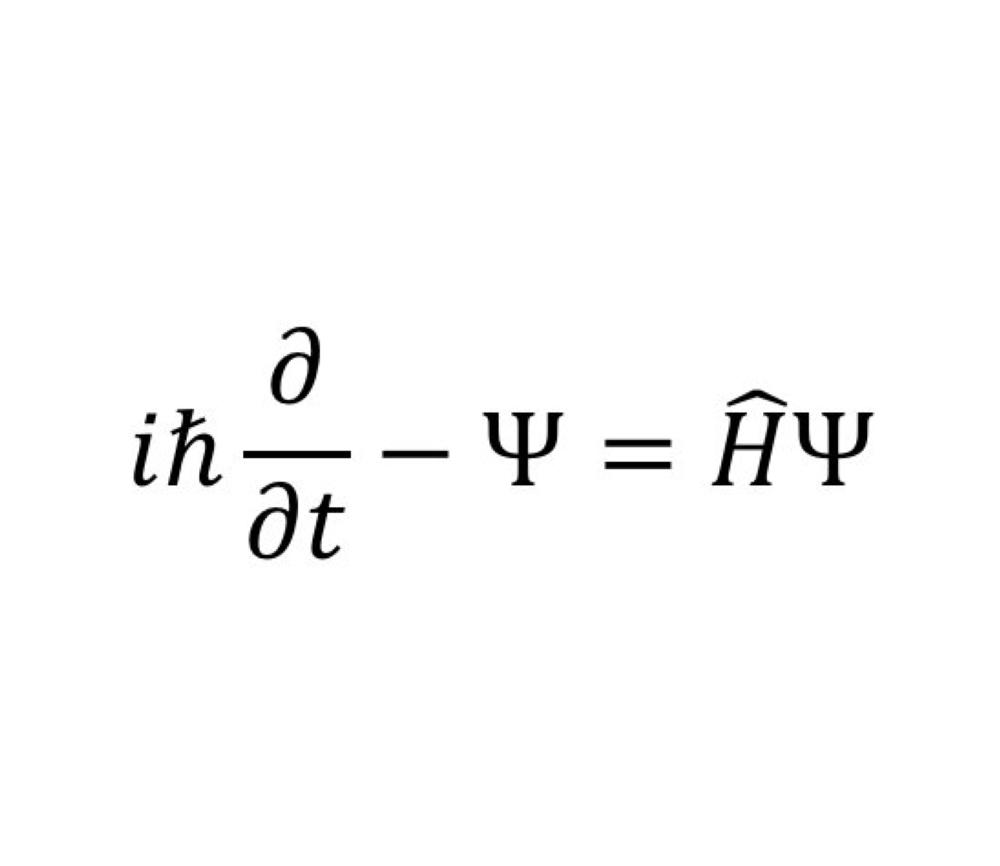لابد أنك تساءلت في حياتك ولو لمرة أثناء مراحل دراستك، وقلت:
ما فائدة دراسة الرياضيات في حياتنا؟
ولا بد أنك سمعت ذلك الجواب اللامنطقي والناقص، بأنها مفيدة في حسابات الأعداد والقياسات، فلو كان الأمر فعلا كذلك لما لزمنا دراسة كل تلك المناهج والمعادلات واكتفينا بدراسة الحساب والقياسات.
إذن لا بد أن نعيد سؤالنا مطالبين بإجابة مقنعة هذه المرة، والإجابة الحقيقية أكبر مما نتوقع،
حيث قيل بأن الرياضيات بفروعها كاملة يمكن أن تغير العالم.
وهذا صحيح، فالرياضيات علم مرن تجده متشابكا مع العلوم الأخرى، مع الكيمياء والفيزياء والطب والهندسة والعمارة والاقتصاد، العلوم التي لا يمكن أن تتقدم دون الرياضيات.
كما أن دراستك للرياضيات يعني تدريب دماغك على عمليات عقلية معقدة، وتأهيله لحل المشكلات، والتنقيب عن الأسباب، وترشيح الأفضل، والاستنتاج، والربط السريع.
ولا بد أن أكثر ما شككت بفائدة دراسته في الرياضيات هي المعادلات، لذا نقدم لك هنا أشهر المعادلات مع إجابات مدهشة ستغيّر رأيك في الرياضيات للأبد، وسيصبح مخجلا أن تتساءل مرة أخرى عن فائدتها، وذلك بحسب " Business Insider".
1 معادلة فيثاغورس:

هي نظرية في الهندسة الإقليدية، تنص على أنه في أي مثلث قائم الزاوية يكون مجموع مربع طول الضلعين المحاذيين للزاوية القائمة مساويا لمربع طول الوتر.
سميت هذه المعادلة هكذا نسبة إلى العالم "فيثاغورس"، الذي كان رياضيا وفيلسوفا وعالم فلك في اليونان القديمة.
ونص المعادلة هو: في مثلث قائم الزاوية، مربع طول الوتر يساوي مجموع مربعي طولي الضلعين المحاذيين للزاوية القائمة.
الأهمية:
تكمن أهمية المعادلة في أن أغلب تطبيقات الملاحة المستخدمة في عالمنا المعاصر ما زالت تستخدمها من أجل تحديد مواقع السفن والطائرات ومساراتها بدقة، كما تُعدُّ النظرية أحد أهم الأساسيات التي يعتمد عليها رسم الخرائط الجغرافية بشتى أنواعها.
2 اللوجاريتمات:

هي موضوع أساس في علم الرياضيات كما أنها أساسية في عمل وتنظيم برامج الحاسوب، وفي الكثير من القوانين العلمية الهامة، مثل: حساب أعمار الصخور، وعمر الكون، وأعمار اللوحات والآثار القديمة، ودرجة الحموضة وغيرها.
دخل مفهوم اللوجاريتمات إلى الرياضيات في أوائل القرن السابع عشر، على يد العالم "جون نابير" كوسيلة لتبسيط الحسابات.
الأهمية:
تكمن أهمية اللوجاريتمات في كونها طريقة ثورية لضرب الأرقام مرات متعددة في معادلة واحدة، لذلك صنعت نقلة نوعية في علم الفلك وتسيير المركبات، ورغم كون أهميتها تراجعت بعد ذلك بسبب ظهور وسائل تقنية أكثر دقة.
3 النظرية الأساسية التفاضل والتكامل:

هي فرع من فروع الرياضيات والتي تطورت بشكل خاص على يد "إسحاق نيوتن". وتدرس النهايات والاشتقاق والتكامل والمتسلسلات اللانهائية، وهو علم يستخدم لدراسة التغير في الدوال وتحليلها.
ويدخل علم التفاضل والتكامل في العديد من التطبيقات في الهندسة والعلوم المختلفة، حيث كثيراً ما يحتاج لدراسة سلوك الدالة والتغير فيها وحل المشاكل التي يعجز علم الجبر عن حلها بسهولة.
الأهمية:
تتعلق النظرية بشكل رئيسي بحسابات نهايات الدوال الرياضية، وتستخدم بشكل موسع في رسم المنحنيات الرياضية الخاصة بمختلف العلوم، كالإحصاء والاقتصاد وعلوم الحاسب بل والطب أحيانًا.
4 قانون نيوتن للجاذبية:

هو كما يعرف اختصارا بقانون الجذب العام، وهو قانون فيزيائي استنباطي ينص على أنه "توجد قوة تجاذب بين أي جسمين في الكون، تتناسب طرديًا مع حاصل ضرب كتلتيهما، وعكسيًا مع مربع المسافة بين مركزيهما"
الأهمية:
تراجعت أهميته مع ظهور النظرية النسبية العامة لأينشتاين، وتطبيقاته واضحة وكثيرة في عملية تسيير الأجسام والمركبات من أجل حساب قوى الجذب بينها.
ولا يزال أحد أهم الأعمدة العلمية من أجل رسم مسارات سفن الفضاء، كما يستخدم بشكل موسع في تحديد مدارات الأقمار الصناعية الخاصة بالبث التليفزيوني.
5 الأعداد المركبة:

هي العدد المركب، وأي عدد ع يمكن كتابته على الصورة: ع = أ +ب ت حيث أ، ب هي أعداد حقيقية، وت = جذر ال -1 ويسمى أ الجزء الحقيقي من العدد المركب، وب الجزء التخيلي من العدد المركب
وأول إشارة سريعة إلى الجذور المربعة للأعداد قد تعود إلى عالم الرياضيات "هيرو السكندري".
أهميتها:
تستخدم الأعداد المركبة في العديد من التطبيقات التي تدخل في حياتنا، كالكهرباء، والديناميكا، والنظرية النسبية، وميادين الفيزياء المختلفة، وهذه الأعداد هي أعداد مرنة لها القدرة على الوصول إلى النتيجة النهائية بشكل مرض.
وتستخدم بشكل موسع في معظم التطبيقات التكنولوجيا الحديثة، من الإضاءة الكهربائية للكاميرات الرقمية إضافة إلى استخدامات متعددة في مجال الهندسة الكهربية.
6 صيغة أويلر للوجوه المتعددة:

تعرف بهذا الاسم نسبة إلى العالم "يونارد أويلر"، وهي صيغة رياضية في التحليل المركب تحدد العلاقة الوثيقة بين الدوال المثلثية والدالة الأسية المركبة.
الأهمية:
تعد أهم أساسات علم الطوبوجرافيا "رسم التضاريس"، كما استخدمت في رسم خرائط الحمض النووى DNA.
7 المعادلة الموجية لبيرنولي:

هي المعادلة الموجية في الفيزياء، وهي معادلة تفاضلية جزئية من الدرجة الثانية تصف بشكل عام حركة الأمواج سواء كانت أمواجا صوتية أو ضوئية أو مائية.
الأهمية:
تستخدم المعادلة بشكل كبير في تحديد أماكن التكوينات الجيولوجية المتعلقة بالنفط، كما تُستخدم في تقدير التفجيرات الأرضية التي يتم افتعالها بهدف التنقيب عن البترول والمعادن.
8 تحويلات فورييه:

هي عملية رياضية تستخدم لتحويل دالّة رياضية بمتغير حقيقي وذات قيم مركّبة إلى دالّة أخرى من نفس الطراز.
الأهمية:
المعادلة أساس لعلم تحليل الإشارات وضغط معلومات الصور في صيغ بسيطة كـJEPG إضافة لرسم بنية الجزيئات، وتُعدُّ امتدادًا لمعادلة بيرنولي السابقة.
9 معادلات نافيير ستوكس:

هي معادلات غير خطية تصف حركة الموائع النيوتونية، حيث تحدد مثلا حركة الهواء، التيارات البحرية، تسرب المياه عبر الأنابيب. أخذت هذه المعادلات اسمها من فيزيائيين هما "كلود نافييه" و"جورج جابرييل ستوكس" من القرن 19.
الأهمية:
تعد من أهم المعادلات في علم الفيزياء، وتستخدم بشكل موسع في تحريك المركبات الهوائية، وتعد أهم المعادلات المستخدمة في تطبيق حركة الطائرات.
10 معادلة ماكسويل:

هي عبارة عن أربع معادلات تفاضلية جزئية، تصف سلوك وتغيرات المجالين الكهربائي والمغناطيسي، وتأثراتهما مع المادة، وتحولاتهما إلى أشكال أخرى من الطاقة.
وقد نشر الفيزيائي "جيمس كلارك ماكسويل" هذه المعادلات بين عامي 1861-1862م، وهذه المعادلات تصف العلاقات المتبادلة بين كل من المجالات الكهربائية والمجالات المغناطيسية والشحنات الكهربائية والتيار الكهربائي.
نص قانون ماكسويل في الكهرومغناطيسية: إذا انتقلت دائرة أو جزء من دائرة كهربائية مغلقة ضمن مجال مغناطيسي منتظم، فإنها تبذل شغلا يساوي شدة التيار الكهربائي المارة فيها في تغير التدفق المغناطيسي الذي يجتازها.
الأهمية:
تعد الكهرومغناطيسية أساس العديد من التقنيات الحديثة في مجال الاتصالات، كالرادار والتليفزيون وعمليات البث.
11 القانون الثاني للديناميكا الحرارية:

هو ما يصف خاصيات وسلوك انتقال الحرارة وإنتاج الشغل، سواء كان شغلا ديناميكيا حركيا، أم شغلا كهربائيا من خلال عمليات ثرموديناميكية.
ومنذ وضعت هذه القوانين أصبحت قوانين معتمدة ضمن قوانين الفيزياء والعلوم الفيزيائية (كيمياء، علم المواد، علم الفلك، علم الكون).
الأهمية:
يتناول القانون العلاقة بين الشغل والحرارة، ويعتبر القانون أساس عمل المحركات البخارية التي صاحبت الثورة الصناعية الكبرى في أوروبا، كما استخدم القانون في إثبات تكون المادة من ذرات عبر استخدام العلاقة بين الشغل والحرارة.
12 النظرية النسبية لأينشتاين:

هي من أشهر نظريات الفيزياء الحديثة، تم تطويرها من قبل "ألبرت أينشتاين" في بدايات القرن العشرين.
توجد نظريتان للنسبية، الأولى هي النسبية الخاصة، والثانية هي النسبية العامة. كلتاهما تعتمد على مبدأ النسبية الذي وضعه "جاليليو جاليلي" في عام 1636م.
الأهمية:
تعد المعادلة الأكثر تأثيرا في التاريخ، ولم لا؟ وهي تعدُ الأساس العلمي الذي بنيت عليه فكرة القنبلة الذرية بكل ما ترتب عليها من آثار.
13 معادلة شرودنجر:

هي عبارة عن معادلة تفاضلية جزئية تصف كيفية تغير الحالة الكمية لنظام فيزيائي مع الزمن، وقد صاغها عالم الفيزياء النمساوي "إرفين شرودنجر" في أواخر عام 1925م، ونشرها عام 1926م.
تصف هذه المعادلة حالات النظم الكمومية المعتمدة على الزمن، وتحتل هذه المعادلة أهمية خاصة في ميكانيكا الكم، حيث تعد بمثابة قانون التحريك الثاني لنيوتن الذي يعتبر أساسيا في الفيزياء الكلاسيكية.
الأهمية:
تعد المعادلة أساس العديد من التطبيقات الالكترونية الحديثة، كالترانزستور وأشباه الموصلات، ويعزى لها الفضل في النقلات الكبيرة نحو استخدام الحاسب الآلي.
14 معادلة شانون للمعلومات:
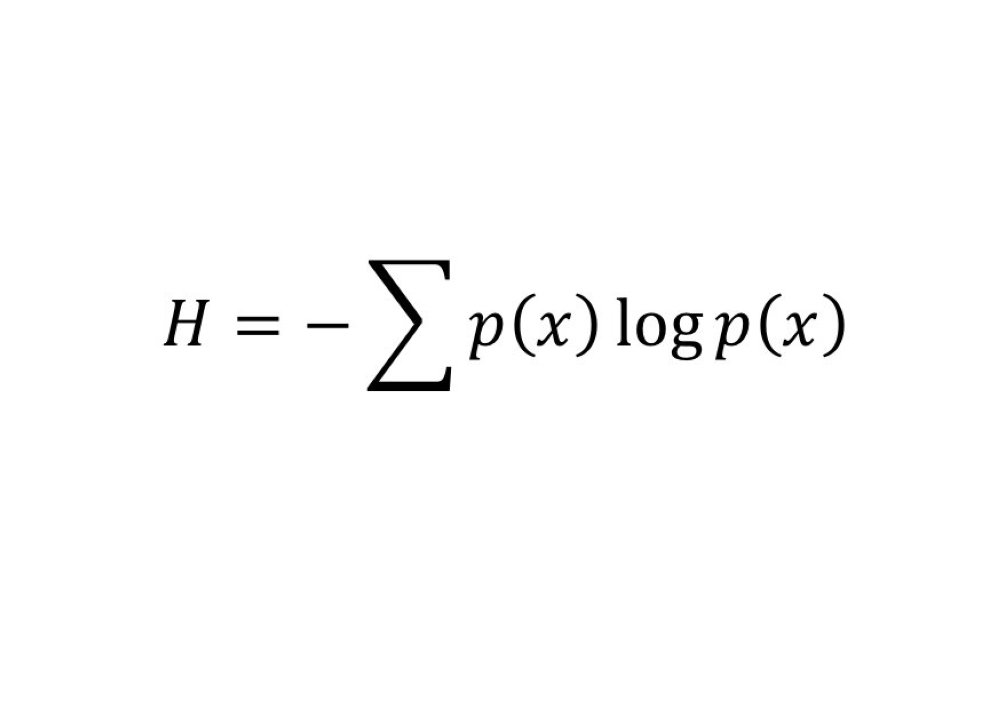
هي أحد تخصصات وفروع الرياضيات التطبيقية الذي يتضمن كمية Quantification (التحويل إلى كميات) البيانات بهدف تمكين نقل أو تخزين البيانات ضمن وسط ما أو نقلها عبر قناة اتصال ما بأكبر قدر ممكن.
الأهمية:
تعد المعادلة أولى مبشرات عصر المعلومات الرقمية، بداية من الأسطوانات المدمجة إلى الاتصالات الرقمية.
15 النموذج اللوجستي للنمو السكاني:

هو نوع شائع من منحنى "سقمويند"، وقد أعطيت الدالة اللوجستية هذا الاسم في أحد عامي 1844 أو 1845 من قبل "بيير فرانسوا فيرهلست"، والذي درس علاقة هذا المنحنى بنمو السكان.
الأهمية:
تستخدم المعادلة في التنبؤ بالهزات الأرضية والتغيرات المناخية طويلة الأجل.
16 معادلة بلاك – شولز:

هي نموذج رياضي للسوق المالية يحتوي على أدوات استثمارية اشتقاقية.
الأهمية:
ساهمت المعادلة في إيجاد سوق مشتقات مالية تصل إلى تريليون دولار، ولكن يعتقد أن سوء استخدام المعادلة أدى إلى نشوء الأزمة المالية العالمية.
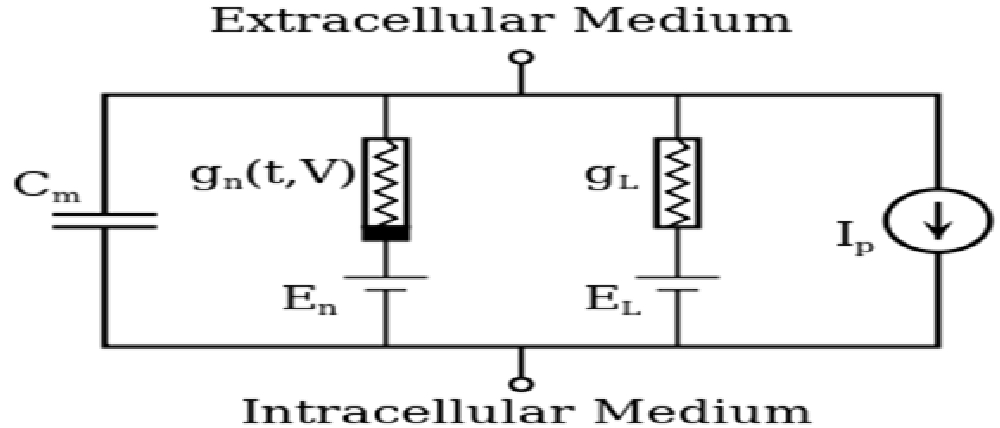
17 معادلة هودجكن- هيكسلي:

هي عبارة عن مجموعة معادلات تفاضلية لا خطية، التي تقرّب الخصائص الكهربائية للخلايا المُستثارة مثل العصبونات وخلايا القلب.
الأهمية:
تعد المعادلة طفرة في تأسيس علم البيولوجيا الرياضية، فقد استخدمت المعادلات الرياضية للمرة الأولى في نمذجة طريقة إرسال الإشارات العصبية.
وأصبحت المعادلة جزءًا رئيسيا من علم الأحياء في العامين الأخيرين، ويعتقد أنه سيكون لها استخدامات طبية موسعة خلال العقد المقبل.
ما فائدة دراسة الرياضيات في حياتنا؟
ولا بد أنك سمعت ذلك الجواب اللامنطقي والناقص، بأنها مفيدة في حسابات الأعداد والقياسات، فلو كان الأمر فعلا كذلك لما لزمنا دراسة كل تلك المناهج والمعادلات واكتفينا بدراسة الحساب والقياسات.
إذن لا بد أن نعيد سؤالنا مطالبين بإجابة مقنعة هذه المرة، والإجابة الحقيقية أكبر مما نتوقع،
حيث قيل بأن الرياضيات بفروعها كاملة يمكن أن تغير العالم.
وهذا صحيح، فالرياضيات علم مرن تجده متشابكا مع العلوم الأخرى، مع الكيمياء والفيزياء والطب والهندسة والعمارة والاقتصاد، العلوم التي لا يمكن أن تتقدم دون الرياضيات.
كما أن دراستك للرياضيات يعني تدريب دماغك على عمليات عقلية معقدة، وتأهيله لحل المشكلات، والتنقيب عن الأسباب، وترشيح الأفضل، والاستنتاج، والربط السريع.
ولا بد أن أكثر ما شككت بفائدة دراسته في الرياضيات هي المعادلات، لذا نقدم لك هنا أشهر المعادلات مع إجابات مدهشة ستغيّر رأيك في الرياضيات للأبد، وسيصبح مخجلا أن تتساءل مرة أخرى عن فائدتها، وذلك بحسب " Business Insider".
1 معادلة فيثاغورس:

هي نظرية في الهندسة الإقليدية، تنص على أنه في أي مثلث قائم الزاوية يكون مجموع مربع طول الضلعين المحاذيين للزاوية القائمة مساويا لمربع طول الوتر.
سميت هذه المعادلة هكذا نسبة إلى العالم "فيثاغورس"، الذي كان رياضيا وفيلسوفا وعالم فلك في اليونان القديمة.
ونص المعادلة هو: في مثلث قائم الزاوية، مربع طول الوتر يساوي مجموع مربعي طولي الضلعين المحاذيين للزاوية القائمة.
الأهمية:
تكمن أهمية المعادلة في أن أغلب تطبيقات الملاحة المستخدمة في عالمنا المعاصر ما زالت تستخدمها من أجل تحديد مواقع السفن والطائرات ومساراتها بدقة، كما تُعدُّ النظرية أحد أهم الأساسيات التي يعتمد عليها رسم الخرائط الجغرافية بشتى أنواعها.
2 اللوجاريتمات:

هي موضوع أساس في علم الرياضيات كما أنها أساسية في عمل وتنظيم برامج الحاسوب، وفي الكثير من القوانين العلمية الهامة، مثل: حساب أعمار الصخور، وعمر الكون، وأعمار اللوحات والآثار القديمة، ودرجة الحموضة وغيرها.
دخل مفهوم اللوجاريتمات إلى الرياضيات في أوائل القرن السابع عشر، على يد العالم "جون نابير" كوسيلة لتبسيط الحسابات.
الأهمية:
تكمن أهمية اللوجاريتمات في كونها طريقة ثورية لضرب الأرقام مرات متعددة في معادلة واحدة، لذلك صنعت نقلة نوعية في علم الفلك وتسيير المركبات، ورغم كون أهميتها تراجعت بعد ذلك بسبب ظهور وسائل تقنية أكثر دقة.
3 النظرية الأساسية التفاضل والتكامل:

هي فرع من فروع الرياضيات والتي تطورت بشكل خاص على يد "إسحاق نيوتن". وتدرس النهايات والاشتقاق والتكامل والمتسلسلات اللانهائية، وهو علم يستخدم لدراسة التغير في الدوال وتحليلها.
ويدخل علم التفاضل والتكامل في العديد من التطبيقات في الهندسة والعلوم المختلفة، حيث كثيراً ما يحتاج لدراسة سلوك الدالة والتغير فيها وحل المشاكل التي يعجز علم الجبر عن حلها بسهولة.
الأهمية:
تتعلق النظرية بشكل رئيسي بحسابات نهايات الدوال الرياضية، وتستخدم بشكل موسع في رسم المنحنيات الرياضية الخاصة بمختلف العلوم، كالإحصاء والاقتصاد وعلوم الحاسب بل والطب أحيانًا.
4 قانون نيوتن للجاذبية:

هو كما يعرف اختصارا بقانون الجذب العام، وهو قانون فيزيائي استنباطي ينص على أنه "توجد قوة تجاذب بين أي جسمين في الكون، تتناسب طرديًا مع حاصل ضرب كتلتيهما، وعكسيًا مع مربع المسافة بين مركزيهما"
الأهمية:
تراجعت أهميته مع ظهور النظرية النسبية العامة لأينشتاين، وتطبيقاته واضحة وكثيرة في عملية تسيير الأجسام والمركبات من أجل حساب قوى الجذب بينها.
ولا يزال أحد أهم الأعمدة العلمية من أجل رسم مسارات سفن الفضاء، كما يستخدم بشكل موسع في تحديد مدارات الأقمار الصناعية الخاصة بالبث التليفزيوني.
5 الأعداد المركبة:

هي العدد المركب، وأي عدد ع يمكن كتابته على الصورة: ع = أ +ب ت حيث أ، ب هي أعداد حقيقية، وت = جذر ال -1 ويسمى أ الجزء الحقيقي من العدد المركب، وب الجزء التخيلي من العدد المركب
وأول إشارة سريعة إلى الجذور المربعة للأعداد قد تعود إلى عالم الرياضيات "هيرو السكندري".
أهميتها:
تستخدم الأعداد المركبة في العديد من التطبيقات التي تدخل في حياتنا، كالكهرباء، والديناميكا، والنظرية النسبية، وميادين الفيزياء المختلفة، وهذه الأعداد هي أعداد مرنة لها القدرة على الوصول إلى النتيجة النهائية بشكل مرض.
وتستخدم بشكل موسع في معظم التطبيقات التكنولوجيا الحديثة، من الإضاءة الكهربائية للكاميرات الرقمية إضافة إلى استخدامات متعددة في مجال الهندسة الكهربية.
6 صيغة أويلر للوجوه المتعددة:

تعرف بهذا الاسم نسبة إلى العالم "يونارد أويلر"، وهي صيغة رياضية في التحليل المركب تحدد العلاقة الوثيقة بين الدوال المثلثية والدالة الأسية المركبة.
الأهمية:
تعد أهم أساسات علم الطوبوجرافيا "رسم التضاريس"، كما استخدمت في رسم خرائط الحمض النووى DNA.
7 المعادلة الموجية لبيرنولي:

هي المعادلة الموجية في الفيزياء، وهي معادلة تفاضلية جزئية من الدرجة الثانية تصف بشكل عام حركة الأمواج سواء كانت أمواجا صوتية أو ضوئية أو مائية.
الأهمية:
تستخدم المعادلة بشكل كبير في تحديد أماكن التكوينات الجيولوجية المتعلقة بالنفط، كما تُستخدم في تقدير التفجيرات الأرضية التي يتم افتعالها بهدف التنقيب عن البترول والمعادن.
8 تحويلات فورييه:

هي عملية رياضية تستخدم لتحويل دالّة رياضية بمتغير حقيقي وذات قيم مركّبة إلى دالّة أخرى من نفس الطراز.
الأهمية:
المعادلة أساس لعلم تحليل الإشارات وضغط معلومات الصور في صيغ بسيطة كـJEPG إضافة لرسم بنية الجزيئات، وتُعدُّ امتدادًا لمعادلة بيرنولي السابقة.
9 معادلات نافيير ستوكس:

هي معادلات غير خطية تصف حركة الموائع النيوتونية، حيث تحدد مثلا حركة الهواء، التيارات البحرية، تسرب المياه عبر الأنابيب. أخذت هذه المعادلات اسمها من فيزيائيين هما "كلود نافييه" و"جورج جابرييل ستوكس" من القرن 19.
الأهمية:
تعد من أهم المعادلات في علم الفيزياء، وتستخدم بشكل موسع في تحريك المركبات الهوائية، وتعد أهم المعادلات المستخدمة في تطبيق حركة الطائرات.
10 معادلة ماكسويل:

هي عبارة عن أربع معادلات تفاضلية جزئية، تصف سلوك وتغيرات المجالين الكهربائي والمغناطيسي، وتأثراتهما مع المادة، وتحولاتهما إلى أشكال أخرى من الطاقة.
وقد نشر الفيزيائي "جيمس كلارك ماكسويل" هذه المعادلات بين عامي 1861-1862م، وهذه المعادلات تصف العلاقات المتبادلة بين كل من المجالات الكهربائية والمجالات المغناطيسية والشحنات الكهربائية والتيار الكهربائي.
نص قانون ماكسويل في الكهرومغناطيسية: إذا انتقلت دائرة أو جزء من دائرة كهربائية مغلقة ضمن مجال مغناطيسي منتظم، فإنها تبذل شغلا يساوي شدة التيار الكهربائي المارة فيها في تغير التدفق المغناطيسي الذي يجتازها.
الأهمية:
تعد الكهرومغناطيسية أساس العديد من التقنيات الحديثة في مجال الاتصالات، كالرادار والتليفزيون وعمليات البث.
11 القانون الثاني للديناميكا الحرارية:

هو ما يصف خاصيات وسلوك انتقال الحرارة وإنتاج الشغل، سواء كان شغلا ديناميكيا حركيا، أم شغلا كهربائيا من خلال عمليات ثرموديناميكية.
ومنذ وضعت هذه القوانين أصبحت قوانين معتمدة ضمن قوانين الفيزياء والعلوم الفيزيائية (كيمياء، علم المواد، علم الفلك، علم الكون).
الأهمية:
يتناول القانون العلاقة بين الشغل والحرارة، ويعتبر القانون أساس عمل المحركات البخارية التي صاحبت الثورة الصناعية الكبرى في أوروبا، كما استخدم القانون في إثبات تكون المادة من ذرات عبر استخدام العلاقة بين الشغل والحرارة.
12 النظرية النسبية لأينشتاين:

هي من أشهر نظريات الفيزياء الحديثة، تم تطويرها من قبل "ألبرت أينشتاين" في بدايات القرن العشرين.
توجد نظريتان للنسبية، الأولى هي النسبية الخاصة، والثانية هي النسبية العامة. كلتاهما تعتمد على مبدأ النسبية الذي وضعه "جاليليو جاليلي" في عام 1636م.
الأهمية:
تعد المعادلة الأكثر تأثيرا في التاريخ، ولم لا؟ وهي تعدُ الأساس العلمي الذي بنيت عليه فكرة القنبلة الذرية بكل ما ترتب عليها من آثار.
13 معادلة شرودنجر:

هي عبارة عن معادلة تفاضلية جزئية تصف كيفية تغير الحالة الكمية لنظام فيزيائي مع الزمن، وقد صاغها عالم الفيزياء النمساوي "إرفين شرودنجر" في أواخر عام 1925م، ونشرها عام 1926م.
تصف هذه المعادلة حالات النظم الكمومية المعتمدة على الزمن، وتحتل هذه المعادلة أهمية خاصة في ميكانيكا الكم، حيث تعد بمثابة قانون التحريك الثاني لنيوتن الذي يعتبر أساسيا في الفيزياء الكلاسيكية.
الأهمية:
تعد المعادلة أساس العديد من التطبيقات الالكترونية الحديثة، كالترانزستور وأشباه الموصلات، ويعزى لها الفضل في النقلات الكبيرة نحو استخدام الحاسب الآلي.
14 معادلة شانون للمعلومات:
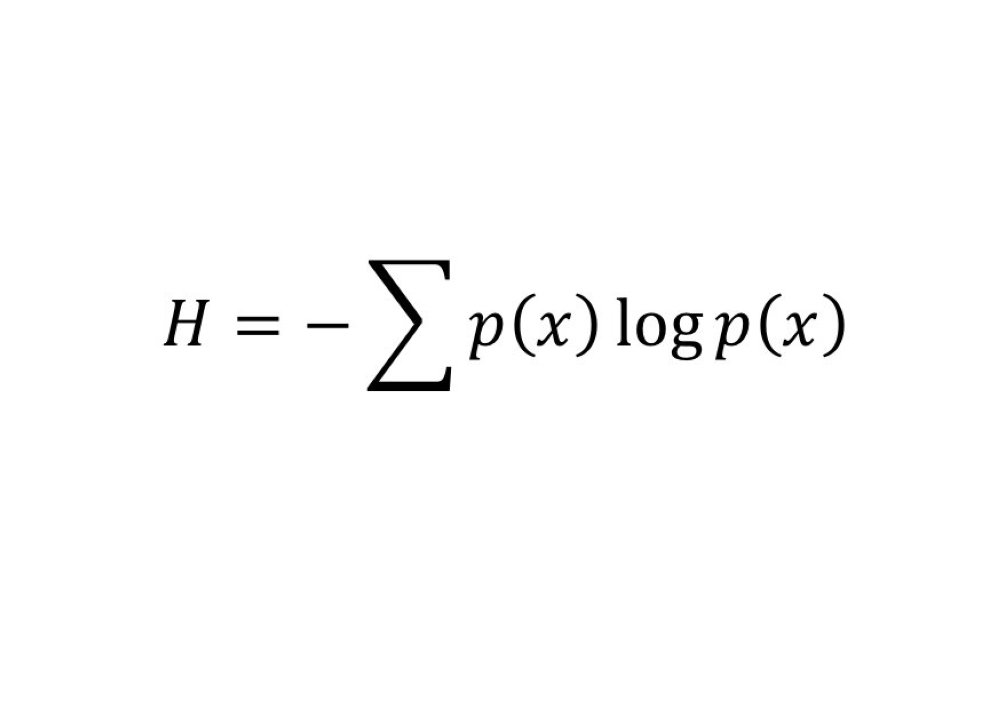
هي أحد تخصصات وفروع الرياضيات التطبيقية الذي يتضمن كمية Quantification (التحويل إلى كميات) البيانات بهدف تمكين نقل أو تخزين البيانات ضمن وسط ما أو نقلها عبر قناة اتصال ما بأكبر قدر ممكن.
الأهمية:
تعد المعادلة أولى مبشرات عصر المعلومات الرقمية، بداية من الأسطوانات المدمجة إلى الاتصالات الرقمية.
15 النموذج اللوجستي للنمو السكاني:

هو نوع شائع من منحنى "سقمويند"، وقد أعطيت الدالة اللوجستية هذا الاسم في أحد عامي 1844 أو 1845 من قبل "بيير فرانسوا فيرهلست"، والذي درس علاقة هذا المنحنى بنمو السكان.
الأهمية:
تستخدم المعادلة في التنبؤ بالهزات الأرضية والتغيرات المناخية طويلة الأجل.
16 معادلة بلاك – شولز:

هي نموذج رياضي للسوق المالية يحتوي على أدوات استثمارية اشتقاقية.
الأهمية:
ساهمت المعادلة في إيجاد سوق مشتقات مالية تصل إلى تريليون دولار، ولكن يعتقد أن سوء استخدام المعادلة أدى إلى نشوء الأزمة المالية العالمية.
17 معادلة هودجكن- هيكسلي:

هي عبارة عن مجموعة معادلات تفاضلية لا خطية، التي تقرّب الخصائص الكهربائية للخلايا المُستثارة مثل العصبونات وخلايا القلب.
الأهمية:
تعد المعادلة طفرة في تأسيس علم البيولوجيا الرياضية، فقد استخدمت المعادلات الرياضية للمرة الأولى في نمذجة طريقة إرسال الإشارات العصبية.
وأصبحت المعادلة جزءًا رئيسيا من علم الأحياء في العامين الأخيرين، ويعتقد أنه سيكون لها استخدامات طبية موسعة خلال العقد المقبل.